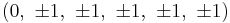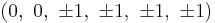Rectified 6-cube
6-cube |
Rectified 6-cube |
Birectified 6-cube |
|
Birectified 6-orthoplex |
Rectified 6-orthoplex |
6-orthoplex |
|
| Orthogonal projections in A6 Coxeter plane | |||
|---|---|---|---|
In six-dimensional geometry, a rectified 6-cube is a convex uniform 6-polytope, being a rectification of the regular 6-cube.
There are unique 6 degrees of rectifications, the zeroth being the 6-cube, and the 6th and last being the 6-orthoplex. Vertices of the rectified 6-cube are located at the edge-centers of the 6-cube. Vertices of the birectified 6-ocube are located in the square face centers of the 6-cube.
Contents |
Rectified 6-cube
| Rectified 6-cube | |
|---|---|
| Type | uniform polypeton |
| Schläfli symbol | t1{4,3,3,3,3} |
| Coxeter-Dynkin diagrams | |
| 5-faces | 76 |
| 4-faces | 444 |
| Cells | 1120 |
| Faces | 1520 |
| Edges | 960 |
| Vertices | 192 |
| Vertex figure | 5-cell prism |
| Petrie polygon | Dodecagon |
| Coxeter groups | B6, [3,3,3,3,4] D6, [33,1,1] |
| Properties | convex |
Alternate names
- Rectified hexeract (acronym: rax) (Jonathan Bowers)
Construction
The rectified 6-cube may be constructed from the 6-cube by truncating its vertices at the midpoints of its edges.
Coordinates
The Cartesian coordinates of the vertices of the rectified 6-cube with edge length √2 are all permutations of:
Images
| Coxeter plane | B6 | B5 | B4 |
|---|---|---|---|
| Graph | |||
| Dihedral symmetry | [12] | [10] | [8] |
| Coxeter plane | B3 | B2 | |
| Graph | |||
| Dihedral symmetry | [6] | [4] | |
| Coxeter plane | A5 | A3 | |
| Graph | |||
| Dihedral symmetry | [6] | [4] |
Birectified 6-cube
| Birectified 6-cube | |
|---|---|
| Type | uniform polypeton |
| Schläfli symbol | t2{4,3,3,3,3} |
| Coxeter-Dynkin diagrams | |
| 5-faces | 76 |
| 4-faces | 636 |
| Cells | 2080 |
| Faces | 3200 |
| Edges | 1920 |
| Vertices | 240 |
| Vertex figure | {4}x{3,3} duoprism |
| Coxeter groups | B6, [3,3,3,3,4] D6, [33,1,1] |
| Properties | convex |
Alternate names
- Birectified hexeract (acronym: brox) (Jonathan Bowers)
Construction
The birectified 6-cube may be constructed from the 6-cube by truncating its vertices at the midpoints of its edges.
Coordinates
The Cartesian coordinates of the vertices of the rectified 6-cube with edge length √2 are all permutations of:
Images
| Coxeter plane | B6 | B5 | B4 |
|---|---|---|---|
| Graph | |||
| Dihedral symmetry | [12] | [10] | [8] |
| Coxeter plane | B3 | B2 | |
| Graph | |||
| Dihedral symmetry | [6] | [4] | |
| Coxeter plane | A5 | A3 | |
| Graph | |||
| Dihedral symmetry | [6] | [4] |
Related polytopes
These polytopes are part of a set of 63 uniform polypeta generated from the B6 Coxeter plane, including the regular 6-cube or 6-orthoplex.
Notes
References
- H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D.
- Richard Klitzing, 6D, uniform polytopes (polypeta) o3x3o3o3o4o - rax, o3o3x3o3o4o - brox,
External links
- Weisstein, Eric W., "Hypercube" from MathWorld.
- Olshevsky, George, Measure polytope at Glossary for Hyperspace.
- Polytopes of Various Dimensions
- Multi-dimensional Glossary